Physics 2056 Assignment # 3W Due: 27 March 2003

1. A laser emits light of wavelength λ. Assuming that this light is due to a transition of an electron in a box from the n=2 state to the n=1 state, find the width of the box L.

SOLUTION

Allowed energies: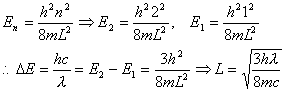

2. A particle bound in a certain one-dimensional potential has a wave function described by the following equations:

(a) Find the value of the normalization constant A.

(b) What is the probability that the particle will be found between x=0 and x=L/4?

SOLUTION

(a) Normalization:

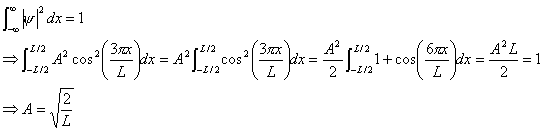
(b)

3. A particle of mass m moves in a potential well of width 2L. Its potential is infinite for x < - L and for x > + L. Inside the region - L < x < + L, its potential energy is given by

In addition, the particle is in a stationary state described by the wave function

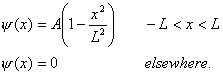
(a) Determine the energy of the particle in terms of , m and L. Hint: Use Schrodinger’s equation.

(b) Show that A = (15/16L)^1/2.

(c) Determine the probability that the particle is located between x = - L/3 and x = + L/3.

SOLUTION

(a) Schrodinger equation:

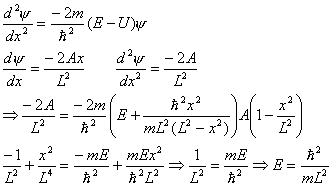
(b) Normalization:

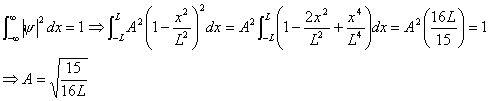
(c)

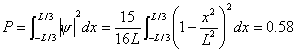
4. Verify that the average value of r for the electron in a ground-state hydrogen atom is 1.5a_o by calculating the expectation value

.

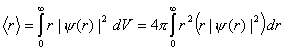Hint: 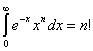where is a positive integer and

SOLUTION

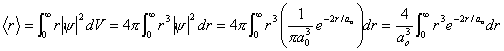
Now let and Then,

5. The Schrodinger equation for the one-dimensional harmonic oscillator is

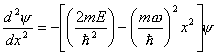
where is the angular frequency of vibration.

(a) Show that satisfies this equation.

(b) Find the value of b and the total energy E.

SOLUTION

Substitute into Schrodinger equation:

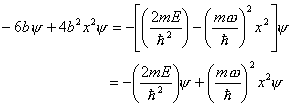
Equate coefficients of powers of x: